TSQL Challenge #18 Blues

I'm working on TSQL Challenge #18, and hitting up against a brick wall. The challenge involves building a calendar for given months of interest (month/year that is). So I build a CTE that first figures out the first & last day of the month, then the week numbers for those days. Matching the week numbers against a tally table, I can then tell which weeks that the days of a particular month will span - those weeks then become rows in the results. I then build a CTE to hold all of my days of interest, with the week number and day-of-month as columns. Using my 'Weeks' CTE as a base, I LEFT JOIN the 'Days' dataset seven times - one for each day of the week.

This is the error I encounter: "The conversion of a char data type to a datetime data type resulted in an out-of-range datetime value." If I limit my day-related tally table to a max of 28 (rather than 31), the error disappears, but I don't get any days in my calendar past the 28th of course. The weird thing is, if I set the tally to max of 31, and I select from the 'Days2' CTE, I don't get an error, and all the days I expect to see are present. Something strange is going on under the hood of SQL.

Kimball Design Tip #119 Updating the Date Dimension

I've always thought of the Time or Date dimension to be a static one, rather than slowly-changing, until I read this tip from Kimball U: "...there are some attributes you may add to the basic date dimension that will change over time. These include indicators such as IsCurrentDay, IsCurrentMonth, IsPriorDay, IsPriorMonth, and so on. IsCurrentDay obviously must be updated each day."

Creating and automatically updating these attributes of the Date dimension will save time (sorry, no pun intended), for report writers and data mart developers, and also standardize such calculations across the enterprise. For example, let's say you are responsible for the data warehouse of a catalog company, and you want to calculate lag time between ordering and shipping, a common metric of customer satisfaction. Furthermore, management decides to give everyone an extra holiday as a bonus for company profitability from last year, and so lets everyone take off Groundhog Day. To account for this in your metric, you are going to want to have an attribute like "BusinessDayOfYear" as an incrementing integer, so that the first business day in January gets assigned BusinessDayOfYear=1, the second day is 2, and so forth, until you have the highest number as the last business day in December (which is most likely Dec 30th). If the company now has Groundhog Day as a holiday, then the IsHoliday for Feb 2nd is changed from 0 to 1, and then the BusinessDayOfYear attribute is recalculated.

Calculating how many business days between ordering and shipping is then trivial. Of course, this does not account for orders placed in December that ship in January, so you might want to have an attribute BusinessDayLifetime, which starts at 1 the first day the company was in business, and increments freely forever.

Building a Yahoo Finance input adapter for SQL Server StreamInsight

Here's an excellent SSC article by Johan Åhlén on building CEP (Complex Event Processing) solutions in SQL 2008. "What is StreamInsight and what is it good for? StreamInsight is a platform for developing and deploying applications that handle high-speed streaming data. It could be used for near real-time processing of data from production environments, structured data such as financial information and unstructured data such as Facebook, Twitter and blogs. Multiple sources can be combined and refined before they are being output. This technology is called CEP - complex event processing.

"Combine StreamInsight with data mining, and you can have real-time fraud detection, stock market prediction, you name it... Imagine a real-time Business Intelligence-application where the management can actually see the KPI gauges moving on the screen. I would say that monitoring real-time flow of information is one of the key success factors for tomorrow's Business Intelligence. This is also supported by Ralph Kimball, saying in an interview that Business Intelligence is moving from the strategic level towards operational level processes such as customer support, logistics and sales. At the operational level data must be continuously updated, not just once per day. I would add also that the new generation, that has grown up with Facebook and Twitter, will make it necessary to monitor new sources for successful Business Intelligence."

Data Vault Institute

While reading the comments on an SSC article about fault-tolerant ETL loading, I came across a link to the Data Vault Institute, and what sparked my attention was the comment by Dan Linstedt that "today's data warehouse has become a system of record. Due in part for the need of compliance." This struck me as an important point, given that many of the databases on which I've worked in the past were marketing databases, where bad data was generally disposed of. But in financial, health care, and governmental data warehouses, this approach would be completely unsatisfactory.

TSQL Challenge #17

"TSQL Challenge 17 - Creating cross rows references with inline hyperlinks" is now out. Due in - a couple of weeks?

Intelligent Keys

I'm engaged in an internal debate about the use of intelligent versus surrogate keys. Typically when this issue arises, the debate centers around whether we want to use a key that is already present in the data (such as SSN in an employee table - this is an intelligent key, also known as a natural key), or if it's better to generate a new meaningless key (such as an auto-incrementing integer - this is a surrogate key).

Now the internal debate isn't over that issue per se - I fall on the side that favors the surrogate key creation. The real debate I'm in is whether it's okay to create an intelligent surrogate key. The most typical surrogate as mentioned previously is an auto-incrementing integer identity - every time a row is inserted into the table, a new key is created by adding one to the max value. These keys have zero business meaning - that's their advantage, that they are decoupled from the business data. However, there are situations where it makes sense to create this value intelligently. One example is creating a time dimension in a data warehouse, whereby the primary key consists of an integer in the form "YYYYMMDD". Microsoft favors this method (as I discovered in their training kit for exam 70-448). A big advantage to this approach is that if you create a clustered index on that intelligent surrogate key, all of your data will be sorted in date order (of course, if you insert into that table by earliest date first, it will also be in that order - unless you add an earlier time period at a later date).

TSQL Challenge #16 Out

I missed it (was out a week ago): http://beyondrelational.com/blogs/tc/archive/2009/11/02/tsql-challenge-16-find-intersections-in-date-ranges-and-concatenate-aggregated-labels.aspx

SQL/ETL/BI 101

I'm going to compile a list of articles that provide introductions to topics in SQL and BI.

Introduction to Indexes, by Gail Shaw

Index of MS-SQL Articles on DatabaseJournal.com, a gold mine of introductory articles.

"What a Data Warehouse is Not" by Bill Inmon.

SSIS Data Cleansing Webinar

I watched a good webinar on SSIS Data Cleansing, by Brian Knight and the good folks of Pragmatic Works of Jacksonville FL. "In this session with SQL Server MVP, Brian Knight, you'll learn how to cleanse your data and apply business rules to your data in SSIS. Learn how to solve complex data problems quickly in SSIS using simple techniques in the data flow. Brian will start by showing you the Data Profiling Task. Then he'll show how to use transforms like Fuzzy Grouping to de-duplicate your data and SSIS scripts to satisfy common scenarios he sees in the industry."

Help, my database is corrupt. Now what?

Found a good article on SSC about database corruption by Gail Shaw:

"What to do when the database is corrupt.

1. Don't panic
2. Don't detach the database
3. Don't restart SQL
4. Don't just run repair.
5. Run an integrity check
6. Afterwards, do a root-cause analysis"
   

Don't have a corrupt database, but still want to play in the sandbox? Click here and here for a couple of ways to corrupt your database. (Don't do this to production data!)

And if all else fails, there's a product called Recovery for SQL Server to help fix your files.

SQL Server Execution Plans

Here's a link on SSC to a free PDF download of Grant Fitchley's "SQL Server Execution Plans", which is, funnily enough, about how to interpret and act upon an execution plan in SQL Server. "Every day, out in the various SQL Server forums, the same types of questions come up again and again: why is this query running slow? Why isn't my index getting used? And on and on. In order to arrive at the answer you have to ask the same return question in each case: have you looked at the execution plan? " – Grant Fritchey

Kimball University: Six Key Decisions for ETL Architectures

SSC posted a link to a good article titled "Kimball University: Six Key Decisions for ETL Architectures", by Bob Becker. Although written for directors/managers, I think developers will also find many of the points useful to understanding the context of an ETL project.

The ‘Subscription List’ SQL Problem

SQL ServerCentral now has a "Stack-Overflow"-type forum for SQL questions, ask.sqlservercentral.com. Phil Factor posted an interesting problem here that asks developers to post solutions to a report on a subscription list.

Celko on Stats

Click here for a really good article by Joe Celko on statistics. He discusses the difference between causation and correlation, and how to compute such things in SQL.

T-SQL Challenge #15

T-SQL Challenge #15 is out. It requires the use of PIVOT; an example can be found on MSDN at the bottom of this entry.

Database Space Capacity Planning

Good article on "Database Space Capacity Planning" by Chad Miller, that uses Powershell to query the space capacity of every SQL Server on your network. From his summary: "The need to monitor and forecast database and volume space is a critical task for database administrators. You can use the process described in this article to create a consolidated space forecasting report, which focuses on a "days remaining" metric. In addition, the use of PowerShell to collect data and load into a SQL table as demonstrated in this article, provides a solution you can easily adapt to many database administration problems."

Are Row Based DBs the Problem in BI?

"Using a traditional, row-based database to run critical reporting and analytics systems is like entering a delivery truck in a Grand Prix race. It's just not what it was designed to do." - Dan Lahl, director of analytics for Sybase. Interesting article by charlesb2k on the pros and cons of transactional, star-schema, and columnar databases for BI and analytics: "Are Row Based DBs the Problem in BI?"

Setting up Change Data Capture in SQL Server 2008

Good article on "Setting up Change Data Capture in SQL Server 2008" by Tim Chapman, TechRepublic. As some of the commentators noted, the article explains how to easily setup CDC in SQL 2008, but provides no help for querying the CDC tables.

How to Calculate Data Warehouse Reliability

Very good article on "How to Calculate Data Warehouse Reliability" by Ashok Nayak. He makes the point that even if every stage in your data warehouse processing has 90%+ reliability, your DW as a whole might only have 70 or 80% reliability. Conventional thinking leads us to believe that every stage is like a link in a chain (where the chain is only as strong as its weakest link), but he concludes that it's much worse than that, that processes P1, P2, and P3, with independent reliabilities R1, R2, and R3, respectively, is not MIN(R1, R2, R3), but is actually R1 * R2 * R3.

T-SQL Challenge #14

T-SQL Challenge #14 is out. I've completed the challenge functionally, now I will tweak my solution to improve performance.

Books by Joe Celko

Excellent article by Wesley Brown that summarizes a bunch of books by the legendary Joe Celko. Don't know Joe? "He has participated on the ANSI X3H2 Database Standards Committee, and helped write the SQL-89 and SQL-92 standards. He is the author of seven books on SQL, and over 800 published articles on SQL and other database topics."

SQL Formatting

Here is a good article on the need to develop formatting standards for T-SQL code within an organization.

TSQL Challenge #12

Click here to view my solution for TSQL Challenge #12, which involves identifying missing dates in a range, and propagating values for those missing dates.

TSQL Challenge #13 - Set-based solution

The set-based solution took me 3 or 4 times as long to develop as the cursor-based solution yesterday. I'm not sure if that's the nature of set-based development, my own learning curve, or both (like going from algebra to calculas). The set-based solution took a couple of interesting tricks to solve, which I will hold off publishing until after the deadline to the challenge.

TSQL Challenge #13

Looking at TSQL Challenge #13, I created a grouping by batch and invoice number:

The most straight-forward approach from here is to insert this into a temp table, open a cursor on it, run through the data and modify the "Set" column so that the batch/invoice numbers are appropriately grouped together. Then join the results of that temp table back to the original data set via batch/invoice number, so that the modified "Set" column is appended. This cursor-based solution is here (the rules require a set-based solution, so I did the cursor-based one just as a baseline to compare to the set-based solution).

Interesting SQL Articles

SQL Server 2008 T-SQL Enhancements Part - I
Celko's Summer SQL Stumpers: Prime numbers
A Simple way of Automating Scripts
Attribute Discretization: Customize Grouping Names

Avoid Logging When Populating a Table

I recently ran into a brick wall while trying to populate a skinny table with just over 130 million rows, in that the log filled up way before the table did (I was down to about 40gb free on my local machine). This is a scenario where I have multiple recursive CTEs preceeding a INSERT .. SELECT FROM used to create those rows. To get around this problem, I created a stored procedure that outputs the results of those CTEs as a straightforward SELECT, then I redirect that output to a text file via a BCP batch file. I then BCP that file back into my destination table, thereby bypassing the extraneous logging that, in this case, is just a waste of space and time.

Cool Use of CTEs to create number table

Many developers have needed to create a numbers table for matching data to ranges, etc., and this article shows various ways to do it, including multiple uses of CTEs: http://www.projectdmx.com/tsql/tblnumbers.aspx

Poker DW: Stacking the Deck Part 2

Earlier we showed how to construct a list of all possible 5 card poker hands, and verified the result in Wikipedia. What I want to create is a table of those hands, all 2,598,960 of them, with their high- and low-hand ranks also. I want to be able to analyze the odds of one hand winning over another with n cards to come, which means that I'll need to create a temp copy of the deck, pull out the known cards from it, and make a hand with every card left and evaluate those hands against my table of all possible.

Now how will I represent the cards in the table of poker hands? The most obvious way is to create a five column key consisting of the 5 CardId values that make that hand. Question: does the order of those CardIds matter? Remember what we talked about last entry, the order should not matter. But we have to put them in some sort of order - if we have five columns, say CardId1, CardId2, CardId3, CardId4, and CardId5, something is going to have to go somewhere. Let's say that we arbitrarily enter the CardIds into the columns in no particular order - how will we now query them? Let's make a trivial example of querying for two cards. Our WHERE clause of such a query would look like:

WHERE CardId1 = @CardId1 AND CardId2 = @CardId2
OR CardId1 = @CardId2 AND CardId2 = @CardId1


We have to match every permutation of variables to columns. With three cards:

WHERE
CardId1 = @CardId1 AND CardId2 = @CardId2 AND CardId3 = @CardId3
OR CardId1 = @CardId1 AND CardId2 = @CardId3 AND CardId3 = @CardId2 OR CardId1 = @CardId2 AND CardId2 = @CardId1 AND CardId3 = @CardId3 OR CardId1 = @CardId2 AND CardId2 = @CardId3 AND CardId3 = @CardId1 OR CardId1 = @CardId3 AND CardId2 = @CardId1 AND CardId3 = @CardId2 OR CardId1 = @CardId3 AND CardId2 = @CardId2 AND CardId3 = @CardId1

Going back to our research on permutations, the number of permutations of n elements is n!, which is also equal to n(n + 1)/2. With five cards we're looking at a WHERE clause that is 5(5+1)/2 = 5*6/2 = 15 lines long. The coding for that isn't so bad (try not to make a mistake - you'll be matching 5 variable/column pairs per line for 15 lines, for a total of 75 equality checks), but think of how slowly that would perform! And that's just to evaluate one hand - imagine the gears grinding away to find all possible 5 card hands with two cards to come - if you're on the flop, and you want to evaluate your chances to the river, you have "47 choose 2" =
1081 possible outcomes.

What I came up with is a solution using prime numbers that I learned while studying Gödel's incompleteness theorems. We assign every card in the deck a unique prime number; the first card gets 2, the second card 3, all the way up to the last card, which gets prime number 239. Now what happens if we want to look at a two-card hand and match it to a table of all possible two-card hands? If we multiply the prime numbers corresponding to those cards, we will get a number that is unique to those two cards (the primes of any other two cards will result in a different number when multiplied). Obviously it doesn't matter which order the primes are multiplied, so we have just found the perfect primary key for our poker hands table. When we want to evaluate a hand, we multiply the primes corresponding to the cards and match the result to the primary key.

We have an updated Dim_Deck creation script that adds a "PrimeFactor" column to it. Now I'm working on a creating the table of all possible hands.

Poker DW: Stacking the Deck

Returning to the Poker Data Warehouse, I dove into the text-parsing process after setting up a sketch of an initial database design, with the idea of polishing out the design at a later date. I recently completed the parsing of a sample hand history, and man was it more work than I expected! Fortunately I love writing text-parsing routines (perhaps from early career work in merge-purge duplicate removal), so the 750 line stored procedure was more a labor of love than a tedious chore. Getting into the dirty details of the source data made me think more about the 30,000 ft overview also.


I created a representation of a 52 card deck of cards in the Poker DW, and I started thinking about how to evaluate 5 card poker hands (i.e., determining what a player had at the end of the hand). What I really want is to be able to evaluate the odds of making the best hand on the next card or the river, which would ultimately allow me to judge whether a player made the right decision. This result would be similar to the "% to win" stats that you see on TV.


After I created my deck of cards, I started playing around with representing a hand of 5 cards. How many possible 5 card hands are there? Easy - think of it like this. Take 1 card from the deck, there's 52 cards to choose from. Take another card, there's 51 to choose from. Keep picking until you have 5 cards in your hand, that leaves 52 * 51 * 50 * 49 * 48 = 311,875,200 possible 5 card hands.


The problem with this method is that I'm picking permutations of 5 card hands, rather than combinations. Let's reduce my example above to picking two cards rather than five. According to that math, there are 52 * 51 = 2,652 possible two card hands. Using the card deck created above, this query will return that count, 2652 rows:


;WITH Draw1 AS (
SELECT Card1 = CardId
FROM Dim_Deck
),
Draw2 AS (
SELECT
Card1,
Card2 = CardId
FROM Dim_Deck D2
JOIN Draw1 D1
ON D1.Card1 <> D2.CardId
)
SELECT COUNT(*) FROM Draw2


Note the use of the recursive CTE to create the second draw, Draw2. So let's say that I picked the five of clubs first, and the four of hearts second. That is one of the 2,652 possible events. But the reversal of that order is also one of the possible events (picking the four of hearts first, and the five of clubs second). But I really don't care which order the two cards come in (the permutation), I only care about the set of cards that results.


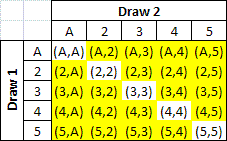
Looking at an even simpler example of a deck of 5 cards, ace to five, how many ways are there to pick two? Here's a simple matrix:

The code above will pick everything except the diagonal that shows pairs:

but what we really want is this:

And in order to get it, we change the "<>" operators to ">":

;WITH Draw1 AS (
SELECT Card1 = CardId
FROM Dim_Deck
),
Draw2 AS (
SELECT
Card1,
Card2 = CardId
FROM Dim_Deck D2
JOIN Draw1 D1
ON D1.Card1 > D2.CardId
)
SELECT COUNT(*) FROM Draw2

and we obtain the correct result, 1326 rows.

StackOverflow

I started answering questions on StackOverflow, and came across a couple of interesting sites. The first is Vyas code page, a small library of useful SQL code. The other is an add-on toolkit for SSMS.

T-SQL to Export Table Structure to a script

Good script for scripting out SQL tables via T-SQL rather than Enterprise Manager/Dev Studio: http://www.sqlservercentral.com/scripts/Miscellaneous/30730/

CRM Import - Importing Into Drop-Down Combobox Targets

During the initial try to load accounts into MS-CRM 4.0, my source file failed for columns that had drop-down combobox columns as targets. A little research lead to this forum post, which advises using the GUIDs of the target system. I was a little mislead by this post, since it actually applied to lookups, not drop-down combobox values. The solution I needed involved converting the source values to the AttributeValue equivalents in the StringMap table of the MS-CRM database.

BCP out Temp Tables

Hit a little snag today trying to output, via BCP, the results of a stored procedure that created and dropped a local temp table. The spd would run fine in Query Analyser, but when run from the DOS prompt I got the error message that the temp table didn't exist. Perhaps the problem is caused by BCP compiling and running the spd in different threads? Anyways, the results of a little googling provide the workaround of keeping the table in TempDb rather than creating as a real temp table. That works as long as the table is not created and dropped within the spd that BCP calls.

Case Study: Poker DW: Reporting Questions

After reviewing the entities and their relationships, we next want to look at some of the questions we might want to answer from the data in our DW. Some possible questions:

• Which players will call a big checkraise on the flop with an overpair?
• What is the actual expected outcome of reraising on the button with a suited connector and bluffing the flop?

Next: ???

Case Study: Poker DW: Entities

Continuing from the introduction, one of the first things we'll have to do in designing our Poker DW (Data Warehouse), is to identify all of the entities of interest. Taking a look at our sample hand history file (ignore the last two lines of HTML code, the hosting company stamped them when I uploaded the file), the first line starts with a sequence number, the format of the game and the datetime stamp of when a particular hand took place. The second line indicates the name of the table, whether it is real or play money, and which seat is the dealer. The next ten or so lines tell us who is in which seat, and what their stack size is (at the beginning of the hand), followed by a line for each player who posts a blind (small, big, and other). So up to now, we've seen such entities as Time, Table, Player, Seat, and Money (stack and pot size).

The next section begins with the header line "*** POCKET CARDS ***". Here we have such information as the hole cards dealt to the player, and all of the preflop action (fold, check, call, or raise). We can identify three more entities here: Betting Stage, Cards and Actions. The next section, "*** FLOP *** [10s 9d 3h]", contains the same entities, but this time we have community cards. At each step in these sections, we can calculate the pot size and stack sizes for each player. Two more sections, "Turn" and "River", provide similar info.

Special consideration should be given to the next section, "*** SHOW DOWN ***", as it will show us exactly what cards other players held during the hand, allowing us to "backfill" that info for earlier rounds of betting. This will help us answer some important questions in the hand histories. The final section, "*** SUMMARY ***", provides info such as the rake, the Hi hand (and Low if this is a hi/lo split game), and the final pot size (which we can use to verify our "running" pot size throughout the hand).

So let's summarize our entities and their relationships. Central to this is Hands. Hands occur at certain Times at a particular Table, which have Seats. Players make Actions with Money based on Cards appearing at a Betting Stage.

Case Study: Data Warehouse for Poker (Intro)

A friend of mine plays a good deal of online poker, and wants to improve his game by studying the hands he has played. I suggested creating a data warehouse from the hand histories held in the text files that the app saves, and using that data to identify winning and losing trends in his game. This entry will serve as the first in a series of the steps we will take to develop this.

Guide to Entries:

• Intro (this entry)
• Identifying Entities
• Reporting Questions

Grouping Datetimes to Identify Sessions

Let's say that I have a record of events that are unique by a datetime "timestamp" marker, and that these events can be grouped by sessions, so that every event that occurs within a certain period of time of the preceeding and/or subsequent events to it are considered as part of the same session. For example, let's say that we are examining cars driving by a traffic counter where each car passing is recorded as an event, and we want to organize the events by sessions so that any two cars passing within 5 seconds of one another constitutes a session (the events will "chain" together so that if four cars pass within 2 seconds of one another, but the first and last cars are within 10 seconds, all four car events are a part of the same session).

Now, if I only have the events, how do I create sessions around them?

Another Version for Calculating Median

Joe Celko published a "history" of calculating the median in SQL, along with a final version that seems to work similarly to mine: http://www.simple-talk.com/sql/t-sql-programming/median-workbench/.

Querying Sys.Columns & Sys.Types

If you want to query the structure of a table that includes column names and data types, you have to perform a join between catalog views Sys.Columns and Sys.Types. There are some caveats to this. If any of your columns are defined as nvarchar or user-defined data types, you must qualify the data coming from Sys.Types. When you add a user-defined data type, it is entered into Sys.Types with a reference to it's native data type. In the example of the AdventureWorks database, the data type "AccountNumber" is defined as nvarchar, and shows up in Sys.Types with system_type_id = 231 (which points to "nvarchar", where system_type_id = 231 and user_type_id = 231).


Running the query:


SELECT
Tb.Name,
C.Name,
Tp.Name
FROM Sys.Tables Tb
JOIN Sys.Schemas Sch
ON Sch.Schema_Id = Tb.Schema_Id
JOIN Sys.Columns C
ON C.Object_Id = Tb.Object_Id
JOIN Sys.Types Tp
ON Tp.System_Type_Id = C.System_Type_Id
WHERE Tb.Name = 'Address'
ORDER BY Tb.Name, C.Name, Tp.Name


produces these results:



Weird, huh? Why did 'AddressLine1' show up six times with six different data types? The reason is two-fold. First, 'AddressLine1' is defined as nvarchar(60), which means that it will also show up as "sysname" datatype (think of "sysname" as MicroSoft's built-in user-defined data type).


Take a look at the results of the query below. It shows that, including itself, six different data types are based on nvarchar! That's why 'AddressLine1' showed up six times in the query above.

SELECT Name FROM Sys.Types Tp
WHERE System_Type_Id = 231

Name
-------------------
nvarchar
sysname
AccountNumber
Name
OrderNumber
Phone
(6 row(s) affected)

So let's change our query to use this 'User_Type_Id' column instead:

SELECT
Tb.Name,
C.Name,
Tp.Name
FROM Sys.Tables Tb
JOIN Sys.Schemas Sch
ON Sch.Schema_Id = Tb.Schema_Id
JOIN Sys.Columns C
ON C.Object_Id = Tb.Object_Id
JOIN Sys.Types Tp
ON Tp.User_Type_Id = C.System_Type_Id
WHERE Tb.Name = 'Address'
ORDER BY Tb.Name, C.Name, Tp.Name

This produces the results we want:

Data Patterns and the LIKE Clause

The "LIKE" clause of the SQL SELECT statement is one of the more interesting features of SQL's character processing. Most everyone is familiar with the "%" wildcard, which allows queries such as "SELECT LastName FROM Customers WHERE LastName LIKE 'Mc%'". This returns all the customer last names beginning with "Mc" (such as yours truly). But I suspect that many developers are unaware of some of the deeper uses of data pattern expressions.

The list of other wildcard characters related to LIKE includes "_", "[", "-", "]", and "^". The first, "_", is the 'any single character' expression. The "[]" characters act as a single character wildcard, but allow us to specify which characters will match. The WHERE clause above is equivalent to "WHERE LastName LIKE '[M][c]%'". When multiple characters reside within the brackets, the filter acts like an "or" expression. So changing the filter to "WHERE LastName LIKE '[M][c][aeiou]%'" would produce last names beginning with "Mc", then followed by a vowel, then any terminating string.

If you use the "-" with the brackets, you can specify ranges of characters (ranges defined by ASCII order). For example, let's say we want to search for user names that begin with 'jmclain' and are then followed by a single digit number. We would execute "SELECT * FROM Users WHERE UserName LIKE 'jmclain[0-9]'".

Where it gets complicated is when you want to search a column for wildcard literals. For example, let's say that you have a column called 'SalesDescription', and you want to count the rows where the SalesDescription column contains the string "50% off". If you were to execute "SELECT COUNT(*) FROM Sales WHERE SalesDescription LIKE '50% off'", you would mistakenly pull in rows with SalesDescription values such as '50 cents off', since the "%" wildcard represents "any string". To correct this, you have two options. The simplest is to enclose the "%" wildcard with brackets, so that the filter changes to "WHERE SalesDescription LIKE '50[%] off'".

The second option is to make use of the ESCAPE clause of the LIKE operator. What this method lacks in simplicity, it make up in robustness (and isn't really that complicated anyways). To solve the above problem suchwise, the filter changes to "WHERE SalesDescription LIKE '50!% off' ESCAPE '!'". I prefer the first method above because 1. it is simpler, and 2. in order to use the ESCAPE clause, you must be certain that your target expression doesn't contain the escape character. So if a given SalesDescription value in the table was, unbeknowst to you, something like '50% off!!!', the results start to become unreliable. Best practices for using ESCAPE stipulate first starting with uncommon characters such as "~" or "", and then querying your column to make sure they are not present.

The best use of ESCAPE is when you want to find brackets in your target. Let's say that you wanted to find the SalesDescription value "[50% off]". After checking to ensure that the column values don't contain the tilde ("~") character, you would use the filter "WHERE SalesDescription LIKE '~[50~% off~]' ESCAPE '~'".

Converting Datetime Values to Varchar

Back when I used to code in Foxpro, I had to write custom code to convert date/time values to various formats. T-SQL provides for a great number of formats using the CONVERT function. An article on MSSQLTips lists many (but not all) of these formats. This code (which can easily be wrapped into a stored procedure), will list out all valid format codes and an example of how they will appear:


SET NOCOUNT ON
CREATE TABLE #Fmts (FmtNo tinyint, Example varchar(max))
DECLARE @fmt int; SET @fmt = 0
DECLARE @dt datetime; SET @dt = GETDATE()
WHILE @fmt < 132
BEGIN
BEGIN TRY
INSERT INTO #Fmts (FmtNo, Example)
VALUES (@fmt, CONVERT(varchar, @dt, @fmt))
END TRY
BEGIN CATCH
PRINT '@fmt = ' + LTRIM(STR(@fmt)) + ' is not valid.'
END CATCH
SET @fmt = @fmt + 1
END
SELECT FmtNo, Example = LEFT(Example, 30) FROM #Fmts
DROP TABLE #Fmts
SET NOCOUNT OFF

And sample output:

Question of the Day

I stumped the gurus on SQLServerCentral.com with another challenging Question of the Day on April 6th, 2009:

Given this code,

DECLARE @val int;
SET @val = -1
CREATE TABLE #empty (val int)

which statement(s) will result in @val being NULL? (select all that apply)

1. SET @val = NULL
2. SELECT @val = NULL FROM #empty
3. SELECT @val = val FROM #empty
4. SELECT @val = (SELECT val FROM #empty)

As of today, only about 30% of respondents answered correctly, and judging from the comments in the discussion section, a lot of them gained a deeper understanding of the concept of null in SQL. I try to make my questions (and answers), tricky enough so as to not be obvious, but my goal isn't to trick people with arcane technicalities - I want to make them aware of certain subtleties of the database engine. This question arose after some unexpected results made me delve into a bit of code, and tested scenarios just like those in the question.

Collation Sequences

Being a database developer rather than a DBA, I rarely deal with collation types, but I came across a situation recently where I had to dig into the issue. My objective was to produce a breakdown of how many rows contained each ASCII character. I considered two approaches: slice the values into one-character chunks, or loop through all 256 ASCII values and count the number of rows containing each character. The former approach has the advantage of not only counting the rows but the frequency of characters (e.g., "100 rows contain 250 instances of the character 'A'"), but I opted for the second approach since it intuitively seemed faster. If your database was created with case-insensitive collation (such as "SQL_Latin1_General_CP1_CI_AS"), checking for the characters 'A', would pull in values of 'a':

USE NorthWind
GO

SELECT DISTINCT City
FROM dbo.Customers
WHERE CHARINDEX('A', City) > 0




To fix, simply add the "COLLATE" clause to the query:

SELECT DISTINCT City
FROM dbo.Customers
WHERE CHARINDEX('A' COLLATE Latin1_General_BIN, City) > 0

"Average" Date

Have you ever tried to calculate the average of a datetime column, and gotten this error:

"Msg 8117, Level 16, State 1, Line 1
Operand data type datetime is invalid for avg operator."

When you first think about it, the error makes sense - are you trying to determine the average month, year, hour, or second? But shouldn't there be such a thing as an "average" date? If we have a bunch of sales orders in a given month, doesn't the "average" date of sale actually mean something?

What if I calculated the MIN value, then calc'd the DATEDIFF between the MIN and all other values? At that point I'd essentially have an integer value, which of course I could average, and then derive the "average" date:

;WITH
CvrtToDate AS (
SELECT
/* "DataValue" is assumed to be varchar(max) */
DataValue = CONVERT(datetime, DataValue)
FROM DataSet
WHERE ISDATE(DataValue) = 1
)
,MinAndMax AS (
SELECT
ValueMin = MIN(DataValue)
,ValueMax = MAX(DataValue)
FROM CvrtToDate
)
,DateDiffs AS (
SELECT
DaysFromMin = DATEDIFF(d, MinAndMax.ValueMin, DataValue)
FROM CvrtToDate, MinAndMax
)
,AvgDaysFromMin AS (
SELECT DataValue = AVG(DaysFromMin)
FROM DateDiffs
)
SELECT
AvgDate = DATEADD(d, AvgDaysFromMin.DataValue, MinAndMax.ValueMin)
FROM MinAndMax, AvgDaysFromMin


This query bears a result that makes sense - we have a date that is between the oldest, and most recent, that is somewhere near the midway point.

A little Google research bears fruit for a much simpler calculation. From "Ask Ben: Averaging Date/Time Stamps In SQL": "The secret to date/time averaging is that date/time stamps can be represented as a floating point number. I have covered this a number of times on this blog so I won't go into too much detail, but the idea is that as a floating point number, the integer part represents the number of days since the beginning of time (as the SQL server defines it) and the decimal part represents the time or rather, the fraction of days. SQL does not make this conversion for you; you have to CAST the date/time stamp as a FLOAT value."

This leads to the revised calculation:

SELECT
ValueMin = MIN(CONVERT(datetime, DataValue))
,ValueMax = MAX(CONVERT(datetime, DataValue))
,ValueAvg = CONVERT(datetime, AVG(CONVERT(float,
CONVERT(datetime, DataValue))))
FROM DataSet
WHERE ISDATE(DataValue) = 1


Not only is this calc far simpler, but it is slightly more precise, as it includes time-of-day in the result.

Calculating Median

I found an article on calculating the median in SQL (http://www.sqlservercentral.com/scripts/Miscellaneous/31775/), and after reading a Wikipedia article on it, I realized that it was incorrect for sample sets of even size. I left a comment with a version of the calc that accounts for this, with a copy of this code:

;WITH
TopHalf AS (
SELECT TOP 50 PERCENT DataValue
FROM DataSet
ORDER BY DataValue ASC
)
,BottomHalf AS (
SELECT TOP 50 PERCENT DataValue
FROM DataSet
ORDER BY DataValue DESC
)
,BottomOfTopHalf AS (
SELECT TOP 1 DataValue
FROM TopHalf
ORDER BY DataValue DESC
)
,TopOfBottomHalf AS (
SELECT TOP 1 DataValue
FROM BottomHalf
ORDER BY DataValue ASC
)
SELECT
Median = (BottomOfTopHalf.DataValue
+ TopOfBottomHalf.DataValue) / 2.0
FROM BottomOfTopHalf, TopOfBottomHalf

Function to Insert Commas Into Number String

While looking into some data quality issues, I considered the case of source data arriving as a string of numbers with embedded commas (for example, "1,526,734.56"), and as I didn't have any such data to test with, I decided to create some, and also created this function in the process (which can be used to create some): fn_AddCommasToNumberString.

(Followup on 4/23/09): A forum post on SQLServerCentral.com explained a very easy way to do this using varchar conversion:

declare @test float
set @test = 7265342.12
select @test, convert(varchar(20),cast(@test as money),1)

SQL Server Data Profiler

With the newest edition of SQL Server, 2008, comes a tool that serves as a good first-cut at providing something for data profiling. Here are some good articles on it:

• A good intro to the Data Profiler tool
• A more detailed look into the tool
• An article that focuses on the payoff
• a look at how to incorporate functional dependency checks between columns
  

Fuzzy Matching

While doing some research on data quality, I came across an article about implementing the Jaro-Winkler distance metric in SSIS. Given two character strings, this algorithm will return a numeric between 0 and 1 indicating similarity (so that 0 is no similarity and 1 means exact match). The Wikipedia entry uses the names MARTHA and MARHTA as an example, producing the result 0.94 (indicating a 94% similarity).

When I ran the comparison of the original versus the most recent versions of the sequence comparisons, I saved the results of the Seq1 and Seq2 tables. While running some tests on the result tables, I discovered a mistake:



The four counts should all be equal, and because they are not, we know that there is a mistake in at least one of them. Because the version 1 results are not even consistent between one another, I have to think that the problem is with the original version.

This query:

SELECT
Seq1_Line = ISNULL(LTRIM(STR(S1.CodeLineNum)), '')
,ISNULL(S1.CodeLineTxt, '')
,ISNULL(S2.CodeLineTxt, '')
,Seq2_Line = ISNULL(LTRIM(STR(S2.CodeLineNum)), '')
,OrderBy = ISNULL(S1.CodeLineNum, S2.CodeLineNum)
FROM Seq1 S1
FULL OUTER JOIN Seq2 S2
ON S1.CodeLineNum = S2.MatchLineNum
ORDER BY OrderBy

will display the matches between the two sequences in a "Windiff"-fashion, and running it on the results of the most recent matching algorithm shows that that one worked correctly.

Comparing Stored Procedures, Part 7

Last week we discovered a set-based method of implementing our sequence-matching algorithm using a Common Table Expression (CTE), and found that it beat our iterative code by several orders of magnitude. Remember the original impetus for this effort, comparing the two stored procedures of more than 1,000 lines each, which initially took about six-and-a-half hours? Running this new version in TempDb on an idle database server took just over 30 seconds! How could this be, given that in Part 6 a comparison of 800 random 2-letter values took about 70 seconds? (Omitted from those results - an input size of 1,000 took over 2 minutes.) How could a test of the same input size (1000 values), but with vastly more complex values (a real stored procedure rather than random two-letter values), take one-quarter of the time to complete? The answer lies in the length of the matching subsequences. If we run this query:

SELECT MatchLineNum, SubSeqLen = COUNT(*)
FROM Seq1
GROUP BY MatchLineNum
ORDER BY COUNT(*) DESC

we get the results:



So on the first matching subsequence, we match 121 values, which is over 10% of the entire sequence. The next matches are composed of 84, 82, 64, and 56 values, which when combined with the first, comprise about 30% of all values. With the sequences of random values, the matching subsequences are much shorter, and therefore requre more executions of the CTE block.

Comparing Stored Procedures, Part 6

In the previous entry, we found that computing the maximum search size prior to the sequence matching using SQL Server 2005's CTE feature saved a considerable amount of time, but we were still performing at an unacceptable rate. I decided it was time to rework the core logic of the matching algorithm. Impressed by the blazing performance of the CTE used to precalculate the max search length, I wanted to recode the algorithm using the set-based logic of the CTE.

Initially using an iterative approach to this problem made a lot of sense, since we need to control the order of the subsequences checked (longer before shorter). There didn't seem to be an obvious way to do this with a CTE. The real power of the CTE comes from its feature of recursion - the ability to have a set of data in the CTE refer to itself (please go here for an excellent article on this). I developed a hybrid approach that would combine iterative and recursive code. The recursive CTE in it will select off the longest matching subsequence between the two sequences it can find whose values are all unmatched, save it in a temp table, and then update the two sequences to show the matching values. It would then continue doing this until no more matching subsequences can be found. This new version can be found here.

The code is much more concise, much more elegant, than the iterative algorithm. But what is truly amazing is the performance increase. After altering the testing script to test all three versions of the code under the same conditions, in the same testing session, the improved performance speaks for itself:

The 'Improved' column compares the latest version with the first. The improved performance represents not just absolute time; notice how slowly the rate of extra time required increases for each increment of the input size. After running the new version for input sizes from 100 to 800 values, I created this graph of the performance time in seconds (graph developed using The Graph Calculator by Holt, Rinehart, and Winston):

The graph rises very slowly at first, then the performance time starts to grow very quickly towards the right end of the graph. Using this website for power regression analysis, we arrive at the approximate formula of y=3.5x^2.5/10^-6. If this is accurate, then the new version is somewhere between square and cubic order of complexity, and although considerably faster than the previous versions, will suffer at larger input sizes.

Next: we examine the results of running our new code on the original large stored procedures.

Comparing Spds, Part 5 - Optimization

Testing out our sequence matching algorithm showed that our estimate of cubic order of complexity was accurate; unfortunately, this performance is what might be called "sub-optimal". If we have any hope of testing our 1,000 line stored procedures in a reasonable timeframe, we're going to have to optimize our algorithm.

The most obvious optimization to make is to simply reduce the number of comparisons, and the way we're going to do that is by checking the sequences ahead of the actual matching. We first check each value in the sequences to see if there exists a match in the other sequence, and then overload the MatchLineNum column to indicate match or no-match. At this point we have a series of subsequences within each sequence of possible matches. But what's important here is the length of the subsequences - the length of the longest subsequence is the maximum search size for that sequence - we need not search for longer ones in it because we already know that longer ones already contain a mismatch. Also, the longest possible matching subsequence between the two main ones will be the smaller of these two maximum lengths.

As an example, let's say that we have two sequences, S1 and S2, and we find that the length of the longest possible subsequences of S1 and S2 is n and m, resp. For the purposes of matching the subsequences between S1 and S2, the maximum subsequence to compare will be of length min(n, m).

The code to determine this maximum subsequence utilizes CTEs, one of the more important enhancements of SQL Server 2005. This was an interesting exercise. I wrote CTEs that first separately picked out the starting and ending points of the subsequences with matching values, constructed the sequences by matching starting and ending points, then calculated the maximum length of these subsequences. CTEs require a set-based approarch, rather than the more algorithmic row-by-row processing; the resulting code is more intuitive, and ultimately more powerful. Please look here for an excellent introductory article to CTEs.

In comparing this improved version against the original code, I tested both with input sizes of 100, 200, 300, 400, and 500, running each code base 5 times for each input size. Here are the results (columns 'Version1' and 'Version2' represent performance time in seconds):

InputSize___Version1___Version2____Improvement
100_________5.064______1.222_______75.9%
200_________48.680_____13.534______72.2%
300_________92.918_____35.958______61.3%
400_________461.862____318.318_____31.1%
500_________614.412____417.818_____32.0%

We can see that the new version improved performance considerably for the smaller input sizes, but peeters out as the size increases. Analyzing the print output from the stored procedure, paying special attention to the @CmprSz values that were output, I can see that the starting compare sizes grew larger as a ratio to the input size as the input size increased. In other words, the larger the sample size the smaller the cost savings. Given that the test sequences consisted of "words" of two letters of the form [A-J][A-J], obviously the larger the sample size the more likely that random values will be shared between the sequences. In two particular runs of the larger sample sets, all values were shared between the two sequences, resulting in zero cost savings.

This is not exactly a failure of testing design - for many real-world scenarios, the likelihood of shared values should follow this trend of increasing as the sample size increases. Consider comparing the words from works of literature - comparing the text of any random two English language authors of the 20th century, the larger the works the more likely that they will share words between them. Another example is DNA - consider the base pairing of AT and GC combinations - since there are only two possibilities in the domain of values, we are certain to find 100% likelihood of shared values between any two DNA sequences (thus reducing our cost savings to zero).

You can find a complete copy of the improved stored procedure here.

Comparing Spds, Part 4 - Performance

In a previous posting, I analyzed the comparison algorithm to determine its complexity, and found it to be of cubic order. The next step is to test the actual performance of the code and see if my estimate was correct. To do this, I wrote a testing script that tests the code several times under several different input sizes (this code can be found here). Using the table in the testing script, I ran a couple more queries to reformat the results to be more suitable for my specific code:

SELECT
InputSize,
NextInputSize = InputSize + 50.0,
NumberOfRuns = COUNT(*),
AveragePercentMatch = AVG(PcntMatch),
AverageRunTime = AVG(CONVERT(decimal(9, 2), CONVERT(varchar(max), DATEDIFF(ss, RunStart, RunDone)) + '.' + CONVERT(varchar(max), DATEDIFF(ms, RunStart, RunDone))))
INTO #AggregatedPerformanceResults
FROM #PerformanceResults
GROUP BY InputSize

SELECT
A.InputSize,
A.AverageRunTime,
ExpectedNextAverageRunTime = POWER(A.NextInputSize / A.InputSize, 3.0) * A.AverageRunTime
FROM #AggregatedPerformanceResults A
JOIN #AggregatedPerformanceResults B ON B.InputSize = A.NextInputSize

and here are the results I saw:


InputSize___AverageRunTime___ExpectedNextAvgRunTime
50__________4.618000_________36.944000_____________
100_________37.270000________125.786250____________
150_________142.642000_______338.114370____________
200_________366.866000_______716.535156____________



The 'ExpectedNextAverageRunTime' values are, as the name indicates, the expected average time of the next input size based on the results of the given input size. This is computed by computing the percentage difference between the given and next input size, cubing it, and multiplying the result by the given average run time. For InputSize = 50, the percentage difference between 100 and 50 is 100/50 = 2, 2 to the third power is 8, times the average run time of 4.618 seconds is 36.944 seconds. Notice that differs only slightly from the actual average run time for InputSize of 100, which is 37.27 seconds. Comparing subsequent expected versus actual average run times shows a similar consistency, which confirms the analysis of the previous posting, that the matching algorithm is of cubic order of complexity.

Next: optimizing the matching algorithm.

Complicated Comments

A "Question of the Day" I submitted to SQLServerCentral.com was published yesterday, and it seemed to generate a lot of interest, due to the rather surprising answer.

The question was, "Given the code below, which numbers will be printed?"

PRINT '1' -- /* ;PRINT '2' */ ;PRINT '3' /*
PRINT '4' --*/
--/*
PRINT '5'
--*/
/*
PRINT '6'
--/*
*/
PRINT '7'
--*/
PRINT '8'

Possible answers:
A. 1, 8
B. 1, 4, 8
C. 1, 4, 5, 8
D. 1, 4, 5, 7, 8

Correct answer: C

Fewer than half of the respondents answered correctly (I certainly would have gotten the question wrong myself - this question derived from research that completely surprised me). It's not exactly a trick question, but the answer centers around a little-known feature of nested comments. It's fairly obvious that the numbers 1, 4, 5, and 8 will print. The tricky part is near the bottom of the code. Most people look at the block comment starting above the line "PRINT '6'" and think that it ends above the line "PRINT '7'", following the reasoning that the line below "PRINT '6'", "--/*" is ignored by the SQL parser. But because the inline comment of that line is already inside a block comment, the inline comment is ignored! Which means that the line "--/*" actually begins a new, nested block comment that closes on the next line, but causes the line "PRINT '7'" to remain commented-out. In other words, the block comment containing "PRINT '6'" also contains "PRINT '7'", and does not close until the line above "PRINT '8'". This confusion explains why, as of right now, 40% of the respondents chose answer "D".

When I submitted the question for publication, I wondered that many people would find it too abstruse and esoteric to be of value. A number of participants in the discussion of the question pointed out that if they saw comments similar to this in a code review, they would send the developer back to his or her desk to clean up. And point taken. Nesting comments in this fashion has very little, if any, upside and almost 100% downside in that it can lead to largely unexpected results. A couple of articles on the site help to establish best practices for commenting: "The case against using single-line comments", by Cade Bryant, and "Worst Practice - Bad Comments", by Andy Warren.

This problem originally came to mind when I started work on a tool for comparing the text from stored procedures. I wanted to allow the option of omitting all comments from the comparison, which of course would require me to identify and parse out comments from the text. In my research, I came across the question of how to treat nested comments - the "order of operation" of inline versus block comments, nested blocks, etc., and that's when I came across the scenario that formed this question of the day. I have to say that I was surprised, almost to the point of shock, that commenting functioned this way.

Comparing Spds Part 3 - Performance

In the previous post, "Comparing Stored Procedures, Part 2," we looked at an algorithm that would match smaller and smaller subsequences between two sequences of interest. When I coded it, I approached it as a proof-of-concept, and thus sidelined any performance concerns. When I tested it on two stored procedures of about 1000 lines a piece on an idle server, the comparison took about 6.5 hours! Some possible reasons why:

• the code is RBAR-based rather than set-based (see this article for a refutation of that)
• there is no indexing of the text elements
• very little optimization has been done

How many comparisons are going on in this algorithm? To figure this out, let's split the accounting between how many subsequences exist, and how those are compared to the other sequence.

Let's say that we have two sequences, N and M, of lengths n and m respectively, where m >= n. Let's take subsequences out of N and compare to M. So how many are there? This count will be denoted by x. If n = 1, then there is only one subsequence, so x = 1. If n = 2, then x = 3 (with sequence 'AB', there is 'AB', 'A', and 'B'). If n = 3, then x = 6. I will omit the proof here, but this results in the simple series (taken from Wikipedia):

If n = 1000, as is the case in my comparison, then x > 500,000! So we have upwards of a half-million comparisons to do already, and we're only counting the left side! Note that this is the worst-case scenario, where none of the elements match between the sequences (any elements contained in a matching subsequence are excluded from future comparisons).

So now the question is, how many subsequences on the right side must we compare to those on the left? Let's look at a simple example comparing strings 'ABC' and 'XYZ':

1. compare subsequences of length 3: ABC:XYZ (1 comparison)
2. compare subsequences of length 2: AB:XY, AB:YZ, BC:XY, BC:YZ (4 comparisons)
3. compare subsequences of length 1: A:X, A:Y, A:Z, B:X, B:Y, B:Z, C:X, C:Y, C:Z (9 comparisons)

The total number of comparisons is 1 + 4 + 9 = 14. Note that the number of comparisons of length n is n^2, and that the sum is another series:

Now let's say that we were comparing 'ABCD' and 'XYZ'. How many extra comparisons does this add (extras highlighted in bold)?

1. compare subsequences of length 3: ABC:XYZ, BCD:XYZ (1 extra comparison)
2. compare subsequences of length 2: AB:XY, AB:YZ, BC:XY, BC:YZ, CD:XY, CD:YZ (2 extra comparisons)
3. compare subsequences of length 1: A:X, A:Y, A:Z, B:X, B:Y, B:Z, C:X, C:Y, C:Z, D:X, D:Y, D:Z (3 extra comparisons)

Does this look familiar? The extra comparisons are the first series summation we saw earlier. And although it certainly adds processing resources, what we are most interested in is the order of complexity, which in our case is


Examining our example comparison of two stored procedures of around 1000 lines each, this results in processing involving on the order of 1 billion comparisons. In an unoptimized algorithm, it's no wonder why this took almost seven hours to complete!

Next: testing our hypothesis in estimating performance.

Comparing Stored Procedures, Part 2

In the previous posting on this topic, Comparing Stored Procedures, Part 1, we found that the stored procedures of interest were more than 90% alike, when counting matching lines of code between them. This result is certainly helpful, but the approach has certain downsides. For example, if the two spds were composed of many blank lines, then we might have a false positive result. If the spds had exactly the same lines, but in different orders, then we would see a 100% match, but we couldn't really say that they were the same. Another thing I was really interested in was, For the lines of matching code, how large were the blocks of matches (matching lines where the next lines matched also)? That sort of result could lead on to something developers familiar with Visual Studio 98 had at their disposal - Windiff, a visual comparison of the spds.


In order to provide this more detailed picture of how the stored procedures matched one another, I devised an algorithm that would compare blocks of lines between them, starting with the largest possible sequence to compare (the size of this would be the number of lines of the smaller spd), and then compare smaller and smaller sequences until the comparison size was just one line (which is what was compared in Comparing Stored Procedures, Part 1). The trick to this approach is that if a match was found between to large sequences of lines, the subsequences in them would never be compared. Although this certainly helps with performance, the real reason behind this is that the fact that large blocks of code matched is very meaningful. Take this example: the string 'ABCD' matches 'ABDC' more than it matches 'DCBA'. How much "more" it matches is the subject of a later posting, where we establish our scoring algorithm.

For a complete list of the code, please go here. The code runs a comparison of the strings "AZXYZBC" and "BCDAEAXYZ" (regarding each letter as a line of code to compare). Because "AZXYZBC" is the smaller string, the size of subsequences to compare starts at its length, 7, and decrements from there. The comparison first checks to see if any instances of "AZXYZBC" are in "BCDAEAXYZ"; obviously there are none, so it next checks for matching subsequences of length 6. No matches are found until it reaches length 3, at which point it finds matches of "XYZ" in both sequences. When it finds that subsequence, it marks each row in the subsequence to indicate the starting matching position in the other sequence; this mark will prevent the letter from being compared again. This allows the comparison to show the matching subsequences in their greatest length, which also indicates the strength of the match.


This image shows the final matching between the sequences:



Notice that row 2 on the left shows no match, even though there is a 'Z' on the right in row 9 - this is because the matching 'XYZ' subsequences are much more important given their longer length.

Next: performance analysis of our algorithm.

Combination of Columns with Unique Values

One of the side projects that I am most proud of is the code I wrote to query a table and return a list of columns comprising a potential unique key, which can be found here. Here's a snippet of the write-up I did for it:

"As an ETL developer, I often receive files in which the natural key is either unidentified or misidentified, and I need to determine a combination of columns that uniquely identifies each row (the natural key, which is usually also the primary or unique key of the table holding this data), in order to integrate the data from that file into the database. Many times it is simply not clear what the unique key should be, and this requires a painstaking cycle of guessing and testing combinations of columns for unique values. To address this problem, I developed a stored procedure that will automatically query the table to discover a candidate for the unique key. At first, I wanted to create a tool that would report all unique combos, but due to performance reasons, I later limited that to just the first one discovered. I added a way to retest and exclude that result if the first one is not satisfactory."

You can also follow this link for the complete article:
http://www.sqlservercentral.com/scripts/T-SQL/62086/

Comparing Stored Procedures, Part 1

I recently completed a data mart requiring me to reproduce, and improve upon, a critical departmental report created in Excel from the results of three stored procedures. These spds appeared to be almost, but not quite identical - they queried similar data sources and output results in identical data structures, using slightly varying processes. I surmised that there was a single stored procedure at one time, that was copied and modified to create the other two, almost like a genetic mutation. Unfortunately all three were actively used - and independently maintained (or not maintained - the risk of keeping duplicate code in use). What would've simplified the analysis greatly is if the original developer had overloaded the original spd to output each of the three result sets, perhaps accepting a parameter to indicate the result of interest.

What I really wanted to know was how similar were the spds, and what made them different from one another? Given that each spd was about 1000 lines long, a casual comparison would not be feasible.

I started my analysis by reading each spd into a table, line by line, so that each row in the table represented a line of code from the spd, and then compared the number of lines from each spd that matched lines in the other spd. Please go here for the complete code.

This produced some interesting results:
spd1: rpt_ReportingSpd1
spd2: rpt_ReportingSpd2
Percentage match between the spds: 92.27%
Percentage of spd1 found in spd2: 94.64%
Percentage of spd2 found in spd1: 90.12%

So based on the raw numbers of lines matching between the stored procedures, they were mostly the same.

Next: an improved algorithm providing more advanced matching.

Welcome to My Blog

I am a database developer focusing on ETL/BI development. My technological background centers on Microsoft SQL Server technologies such as T-SQL programming, SSIS, and SSRS, but also includes Informatica, Visual Foxpro, and application development such as Visual Basic and Java. This weblog will focus on SQL Server, especially T-SQL development and programming. My aim is to present projects and problems in SQL Server and explain my thought process at delivering a solution.

My webpage is http://www.jessemclain.com/, and I can be reached via email at jesse@jessemclain.com. I have contributions on SQL Server Central that can be accessed via the directory at http://www.sqlservercentral.com/Authors/Scripts/Jesse_McLain/413474/.